Tóm tắt
Trong công nghiệp hóa chất, thực phẩm, chế biến và lọc dầu, hay trong các công trình thủy điện, thủy lợi, nông nghiệp kỹ thuật cao và nhiều lĩnh vực khác, việc xây dựng một hệ thống tự động đo và điều chỉnh mức nước là rất quan trọng. Vấn đề đặt ra là cần điều khiển lưu lượng dòng chảy để ổn định mức chất lỏng với độ chính xác cao. Yêu cầu ứng dụng thực tế như vậy, đề tài nghiên cứu đối tượng chính là điều khiển mức nước trong bình đơn.
Với kỹ thuật điều khiển tự động hiện nay thì có nhiều cách để điều khiển mức chất lỏng của hệ thống bồn nước đơn, nhưng ở đây ta sử dụng bộ điều khiển PID kinh điển để điều khiển. Công việc điều khiển được thực hiện mô phỏng trên Matlab, với công cụ là Simulink.
1.1 Các phương pháp mô tả toán học
Mô tả toán học của hệ thống điều khiển tự động và các phần tử của chúng còn có tên gọi là các mô hình toán học. Mô hình chỉ phản ánh những tính chất cơ bản của đối tượng đối với một sự nghiên cửu cụ thể cho trước mà không tính đến những nhân tố cơ bản khác. Điều này dẫn đến vấn đề với cùng một đối tượng ở trong những nghiên cửu khác nhau có thể xuất hiện những mô hình toán học khác nhau.
Trong hầu hết các hệ thống tự động, các quá trình được mô tả bằng các phương trình vi phân, phương trình sai phân, phương trình vi phân – sai phân, phương trình tích phân và các phương trình vi – tích phân.
Các biển trạng thái xi(t), i= 1,n của hệ động học gọi là các biến độc lập, mà tập hợp của chúng đủ để mô tả trọn vẹn trạng thái động học của hệ thống. Điều đó có nghĩa là theo các giá trị cho trước x10, x20,…xn0 của tất cả các biến trạng thái tại một thời điểm xác định nào đó t= t0, theo giá trị cho trước của các tác động ở tất cả các thời điểm tiếp theo t >t0 và theo các phương trình của hệ thống có thể xác định giá trị của tất các biến trạng thái ở bất kỳ thời điểm tiếp theo nào t >t0. Phương trình của hệ thống đối với các biến trạng thái được viết dưới dạng sau:
Trong đó: f1– hàm liên tục, thỏa mãn các điều kiện Lipshits;
u1(t) – tác động điều khiển; z1(t)- tác động nhiễu.
Thông thường số biến trạng thái lớn hơn số biến đầu ra. Trong trường hợp biến đầu ra y1(t) , y2(t),… Yk (t) có thể thể hiện như là hàm biến trạng thái thì phương trình (1.1) được bổ sung thêm phương trình
1. 2 Các tính chất cơ bản của phép biến đổi Laplace
Giả sử hàm f(t) liên tục, khả tích. Ảnh Laplace của f(t) qua phép biến đổi Laplace. Ký hiệu là X(s) được tính theo định nghĩa:
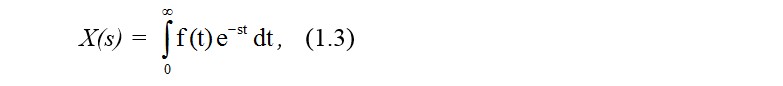
Trong đó, f(t) – hàm biến số thực; hàm X(s)- hàm biến số phức s,
s= α+jω. Khi đó, x(t) được gọi là hàm gốc, còn X(s) gọi là hàm ảnh hay ảnh Laplace.
Vậy, x(t) ⊃ X(s) hay X(s)⊂x(t).
Biến đổi ngược Laplace để xác định hàm gốc ta có thể được viết như sau:
x(t)= L-1{X(s)}. (1,4)
Trong đó, L-1– phép biến đổi ngược Laplace.
MATLAB được ứng dụng để mô phỏng và tính toán, xử lý âm thanh, hình ảnh. Đặc biệt nó còn là công cụ hỗ trợ tốt trong các mô phỏng hệ thống tự động, là công cụ hỗ trỡ đắc lực cho chuyên ngành kỹ thuật điều khiển và tự động hóa. Việc nắm vững cách sử dụng chương trình và ngôn ngữ lập trình MATLAB sẽ là một lợi thế không nhỏ của các bạn sinh viên, nhất là các bạn tham gia vao công việc nghiên cứu khoa học. Bên cạnh đó, công cụ SIMULINK có trong MATLAB là công cụ được nhiều ngành sử dụng với nhiều ứng dụng.
Với các thông số xác định:
+ S = 3m2 – Tiết diện ngang của bồn chứa
+ a = 0,05m2 – Tiết diện ngang van
+ g = 9,81m/s2 – gia tốc trọng trường
+ H0 – 1m – giá trị định mức trong bể
+ k = 0.11 – hệ số tỷ lệ
Kết quả ta thu được:
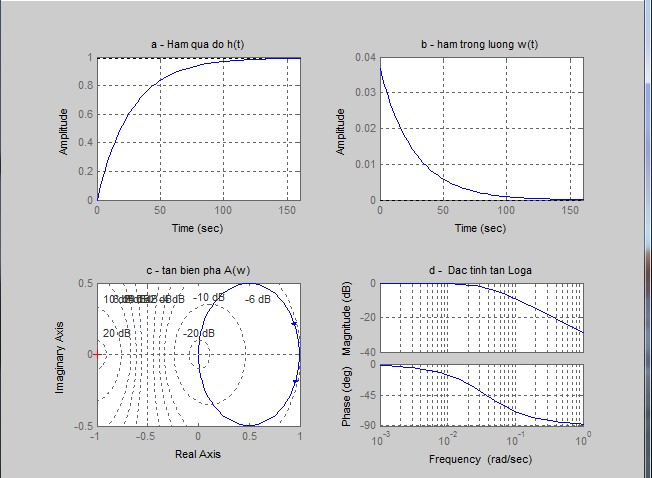
Hình 1
 Nhận xét:
Nhận xét:
+ Quan sát dạng đồ thị hàm quá độ h(t) (hình 1a) và hàm trọng lượng w(t) (hình 1b), so sánh với kết quả vẽ bằng toán học, thấy rằng hai kết quả tương đương nhau.
+ Quan sát kết quả mô phỏng trên (hình 1c) ta thấy rằng biên độ pha của hệ thống hở không bao quanh điểm (-1,0j), và có tọa độ điểm cực nằm bên trái trục ảo. Vậy theo tiêu chuẩn Nyquist thì hệ thống kín ổn định.
+ Ta cũng có thể quan sát (hình 1d) đặc tính tần logarit pha – tần số, nhận thấy rằng nó không cắt đường thẳng đi qua vị trí -II. Nên theo tiêu chuẩn Nyquist hệ thống ổn định.
Để đánh giá hiệu quả làm việc của hệ thống tự động điều chỉnh mức nước dùng bộ điều chỉnh truyền thống PDI, ta sử dụng phần mềm MATLAB, với ứng dụng SIMULINK. Sơ đồ cấu trúc của đối tượng điều khiển được xây dựng trên cơ sở mô hình toán học, được thể hiện trên hình (2) sau:
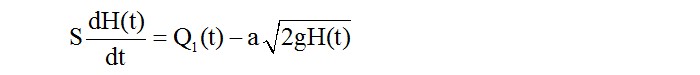
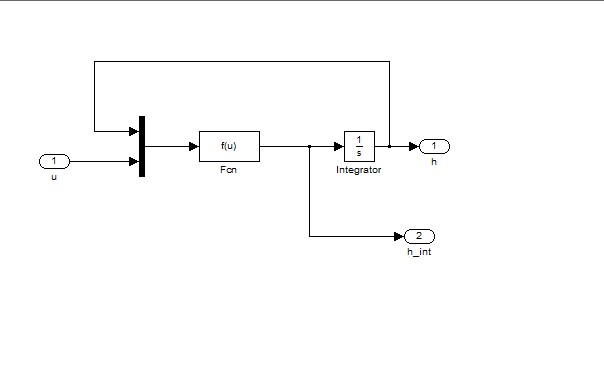
Bộ điều chỉnh PID đảm bảo sự hiệu chỉnh tích phân và sự điều chỉnh phi tĩnh. Độ sai lệch ε(t) được đưa vào bộ điều chỉnh PID, tín hiệu ra của PID được khuếch đại đủ lớn, đáp ứng yêu cầu cho việc điều khiển hoạt động của máy bơm được thể hiện ở hình (3).
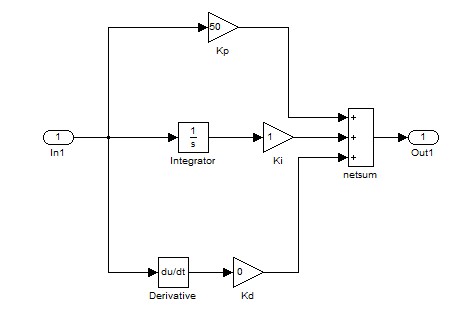
Về tương quan động học, PID tương đương với hệ gồm ba khâu động học mắc song song: Khâu tỷ lệ, khâu tích phân và khâu vi phân. Khi Td =0, bộ điều chỉnh PID trở thành bộ điều chỉnh PI vì thế trong bài này chỉnh ta thưc chất sử dụng bộ điều khiển PI.
Trường hợp 1: Kp=5
H_chuẩn=2m; S=3m2; a=0.025m2; g=9.81m/s2; k=110.
Kết quả hình 4
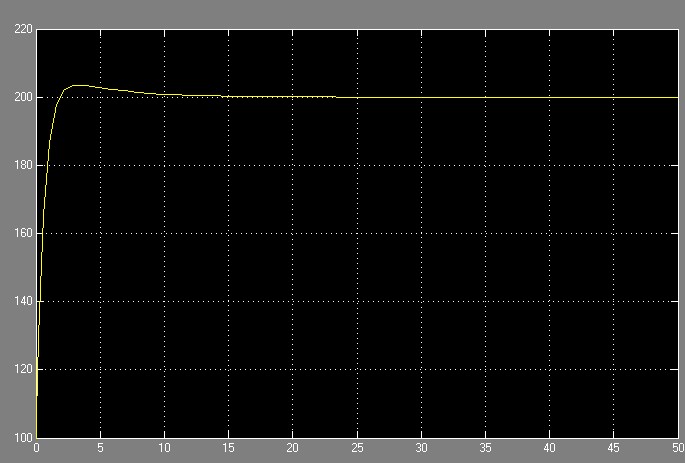
+ Trường hợp 2: Kp=10
H_chuẩn = 2m; S=3m2; a=0.05m2; g=9.81m/s2; k=110.
Kết quả hình 5
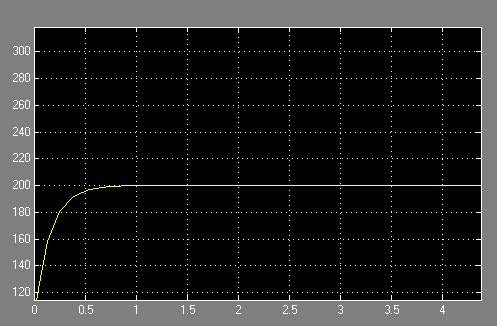
Kết luận
Kết quả mô phỏng cho thấy, khi xác định được các tham số thích hợp của bộ điều chỉnh PID thì quá trình quá độ kết thúc sớm, chất lượng điều khiển của hệ thống được nâng cao. Cụ thể khi tăng Kp càng lớn, nhận thấy quá trình quá độ hệ kín càng nhỏ.
Hệ thống tự động điều chỉnh mức nước được thiết kế trên cơ sở ứng dụng bộ điều chỉnh truyền thống phù hợp với yêu cầu thực tế các quá trình công nghệ trong nhiều lĩnh vực công nghiệp. Kết quả mô phỏng cho trên MATLAB cho thấy hệ thống hoạt động đảm bảo độ tin cậy, độ chính xác, dễ thực hiện kỹ thuật, đơn giản trong công việc hiệu chỉnh các tham số của bộ điều chỉnh.
Tài liệu tham khảo
[1] Nguyễn Doãn Phước (2007), Lý thuyết điều khiển tuyến tính, NXB khoa học và kỹ thuật Hà Nội.
[2] Nguyễn Doãn Phước (2007), Lý thuyết điều khiển phi tuyến, NXB khoa học và kỹ thuật Hà Nội
[3] Nguyễn Doãn Phước (2007), Lý thuyết điều khiển nâng cao, NXB khoa học và kỹ thuật Hà Nội.
[4] Bộ môn Tự động hóa – ĐH bách khoa Hà Nội (2006), Lý thuyết điều khiển tự động
[5] Bộ môn Tự động hóa, ĐH Bách khoa Hà Nội (2006), Mô hình hóa và mô phỏng hệ thống điều khiển tự động
Tiếng Anh:
[6] Gl;enn O.Brown, “The history of the Darcy-Weisbach Equation for Pipe Flow Resistance”, Proceedings of the 150th Anniversary Conference of ASCE Washington, D.C, November, 3-6, 2002, A. Fredrich, and J. Rogers eds., American Society of Civil Engineer, Reston, VA
[7] Harrry L. trentelman – Anton A. Stoorvogel – Malo hautus (2001), Control theory for linear sytems, Springer London.
[8] H Goyal, M hanmandlu and D>P>Kothari (2006), “ A New Optimal Flow Control Approach for Automatic Control of Small Hydro Power Plants”, JIE(I), Vol 87.
[9] “Hydraulic turbine and turbine control moldels for sytsem dynamic studies”. IEEE Transon Power Systems Vol.7. No.1 pp. 167179, Februaary 1992.
Ngô Đăng Lưu (Đại học Quốc Gia Thành phố Hồ Chí Minh)
Nguyễn Đình Long (Trường Đại học Đồng Nai)
Nguyễn Hùng (Trường Đại học Công nghệ Thành phố Hồ Chí Minh)









